这是数据结构课程设计的论文一的分析与理解 翻译,原文可以在这个链接下载。原作者是 Ron Shamir和 Dekel Tsur 。
概要
本片论文的原标题是这个:
Faster Subtree Isomorphism
译成中文则是更快的子树同构,从概要里可以得出,这是在树 $H$ 和树 $G$ 两棵树中进行操作,并且在 $G$ 树中找到一棵与 $H$ 树同构的子树(或是没有)的算法。他们给出了一个时间复杂度为$O(\frac{k^{1.5}}{\log k}n)$的算法,其中 $k$ 和 $n$ 分别是 $H$ 和 $G$ 树的的顶点数。这提高了之前 Chung 和 Matula 的算法(时间复杂度为$O(k^{1.5}n)$)。当然,他们也给出了一个随机化的$O(k^{1.376}n)$时间复杂度的决策算法。
以下是英文原文
We study the subtree ismorphism problem: Given trees $H$ and $G$, find a subtree of $G$ which is isomorphic to $H$ or decide that there is no such subtree. We give an $O((k^{1.5}/{\log k})n)$-time alogorithm for this problem, where $k$ and $n$ are the number of vertices in H and G, respectively. This improves over the $O(k^{1.5}n)$ algorithms of Chung and Matula. We also give a randomized (Las Vegas) $O(k^{1.376}n)$-time algorithm for the decision problem.
正文
介绍
我们知道,图论中有一个基础问题则是图的同构问题,给定两个图 $G$ 和 $H$,找到 $G$ 的一个子图,使得该子图与 $H$ 同构。这是一个 NPH 问题。
NP 问题就是在多项式时间内可以被验证其正确性的问题。如果所有NP问题都可以多项式时间归约到某个问题,则称该问题为NP困难(即 NPH )。
如果我们限制在 $G$ 图中,这个子图同构问题或许会变得更加简单。对于以下问题给出了多项式的时间算法:树、二连通的外部平面图以及串并联图。
外部平面图是一个平面图满足存在一个画在平面上的方法使得外围面的边界包含所有顶点,该画法被称为该图一个外围平面嵌入。外围平面图一定是平面图但反过来不一定成立,例如完全图 $K_4$ 是平面图但并非外围平面图。库拉托夫斯基定理友在外围平面图上的版本:一个图是外围平面图当且仅当它并不包含一个是 $K_4$ 或 $K_{2, 3}$ 的分割的子图。事实上,该版本是下述事实的直接推论:图 $G$ 是外围平面图当且仅当在 $G$ 外面加一个顶点,连边到 $G$ 的所有顶点,所得到的图是平面图。
所有的这些图的节点的儿子数都至多为2。当图 $G$ 满足以上条件时,任意给出的图 $G$ 都使得这个图同构问题是一个NPH问题。(事实上,即使是图 $G$ 每个非树叶节点都有2个儿子并且图 $H$ 为树,他们都只有至多一个节点的度超过3 ,它仍然是一个NPH问题。),甚至当图 $G$ 的路宽为2时亦是如此。不过,对于那些树宽至多为 $p$ 且 $p \geq 2$ 的图来说,这个问题就是多项式的了。

如果我们加入限制条件:图 $G$ 是p连通的,或者图 $H$ 拥有有界的度。一个更快的算法就可以给出。
p连通
对于 $V(G)$ 的每个分割(分成 $X$ 和 $Y$),都存在一个$P_4$,其中$P_4$包含同时存在于 $X$ 和 $Y$ 内的节点。
这个子树同构问题在外部平面图也可以给出多项式时间的算法,或者更广泛的说,在没有 ${K_{3,σ}}$ 图子式的情况下,可以给出。
图子式:在图论中,如果无向图 $H$ 可以通过图$G$ 删除边和顶点或收缩边得到,则称 $H$ 为 $G$ 的子式(minor)或次图。
在这篇文章中我们讨论子树同构问题,也即是当图 $G$ 和图 $H$ 均为树时的情况。图1给出了一个该问题的实例子图同构问题和子树同构问题都在模式识别、计算生物学、化学中有所应用。
模式识别(Pattern recognition),就是通过计算机用数学技术方法来研究模式的自动处理和判读。 我们把环境与客体统称为“模式”。 随着计算机技术的发展,人类有可能研究复杂的信息处理过程。 信息处理过程的一个重要形式是生命体对环境及客体的识别。
计算生物学(Computational Biology)是生物学的一个分支。 根据美国国家卫生研究所(NIH)的定义,它是指开发和应用数据分析及理论的方法、数学建模和计算机仿真技术,用于生物学、行为学和社会群体系统的研究的一门学科。
化学(Chemistry)是自然科学的一种,在分子、原子层次上研究物质的组成、性质、结构与变化规律;创造新物质的科学。
在这个工作中,$n$ 和 $k$ 分别表示了图 $G$ 和 图 $H$ 中的节点数量。当 $k = n$ 时我们得到了线性算法复杂度的树同构问题(基于 Hopcroft 和 Tarjan 的研究成果)多项式时间的子树同构算法首次被 Matula 和 Edmonds 提出。更快的算法又被 Matula 和 Chung 给出。Chung 的算法的时间复杂度为 $O(k^{1.5}n)$。此外,子树同构问题也在 RNC 之中,顾名思义,它可以被一个随机并行算法(Randomized parallel algorithm)在 $\log^{O(1)n}$时间内解决,并且当这个问题限制在对数空间的树中时,它就因此进入 NC 了(?笔者水平问题,意义不明)。与此形成鲜明对比的是,当图 $G$ 是树而 $H$ 是森林时(子森林同构),这个子图同构问题就成了 NPH 了。
森林比树少一个条件,指没有回路的图。也就是说,森林可能是不连通的,边数可能比树还少,就是说小于顶点数。
森林也可以看成是好多棵互不相连的非空的树,只有一棵树也可以算是森林。不过森林不一定是一棵树。
森林也可以是有根的,这时候森林中的每一棵树都有一个根。
一棵树去掉若干条边也会成为森林,这时候可以看成一棵树分成了好多棵树。森林中的两棵树之间加一条边,也可以把这两棵树合在一起,最终合成一棵树。
很多地方用森林,都是用来表示很多棵树,包括作为逻辑结构、数据结构的时候等。有一种重要的数据结构并查集就是一个有根的森林,可以很快的判断两个元素是不是属于同一个互相独立的集合,以及合并两个集合等。
——引用自维基百科
在有根树上的子树同构问题如下:给定两个有根树 $G$ 和 $H$,找到 $G$ 的一个子图 $G’$($G’$ 的根也是 $G$ 的根),在 $H$ 和 $G’$ 之间存在一个同构映射,将 $H$ 的根映射到 $G’$ 的根。这个问题可以在 $O(min(k^{1.5},\sqrt{k}n\log \log n/ \log n)·n)$ 的时间内解决。一个类似的问题是树的模式匹配问题:输入两个有根树 $G$,$H$ 和一串子树值的节点。目标是找到一个从图 $H$ 到图 $G$ 的1-1映射,使得每一个 $H$ 中的节点都能映射到 $G$ 中。在 $v$ 中的第 $i$ 个节点就是 $f(v)$ 中的第 $i$ 个孩子。这个树模式匹配问题可以在 $n \log^{O(1)}$ 的时间内解决。
几个子树同构问题的推广已被研究。在最大相似子树问题中,输入树 ${G_1,… ,G_n}$ ,目标是找到一棵拥有最多节点的树 $H$ ,对于每棵树 $G_i$ 都包含又一个子图与 $H$ 同构。这个问题对于两棵树是多项式的(并且 RNC ),当树的数量达到3棵及以上时,它就成了 NPH 了。 近似的该问题算法已经给出。另一个推广则是最大子森林问题 :查找具有最大边数的给定树的子树,该子树不包含与给定树集中的任何树同构的子图。我们作者的主要成果是一个 $O((k^{1.5}/logk)n)$ 时间的算法。像大多数该问题的研究一样,是基于是基于二部图的子树同构和最大匹配之间的密切关系。将子树同构问题递归地转化为一组较小的子树同构问题,利用最大匹配算法求解。改进的复杂度是通过一个组合引理来实现的,该引理限定了所涉及的不同子树的可能数目,并通过使用团划分的概念以及 Feder 和 Motwani 的应用来确定二部图中的最大匹配。我们证明了对于由子树同构问题产生的匹配问题,我们可以用一种简单的方法找到一个团分区。我们在这里使用的思想,也提出了一个关于最大子森林问题的改进算法。
我们也给出了一个随机化的算法给这个选择问题,期望的运行时间是 $O(k^{ω-1}n)$,式中ω是矩阵乘法的指数。使用已知的最优界给ω,则上界为 $O(k^{1.376}n)$。该算法直接遵循由 Cheriyan 给出的寻找最大匹配基数的随机算法。这个章节的结果发表在另外的论文上。
文章剩下的部分组成如下:第二节描述了一个 $O(k^{1.5}n)$ 的算法。在第3节我们证明了一些简单的在后续章节中需要用的引理。在第4节中,我们证明了组合引理,并将其与团划分结合使用,以提高第二节算法的运行时间。最后第5节描述了这个随机化算法。
我们用一些定义来结束本节内容。对于大多数的定义和基本的图论术语可以查看相关资料。一棵有根树是一个三联体 $G=(V,E,r)$,其中 $(V,E)$ 是一个无根树,$r$ 是 $V$ 中的一些称作“根”的节点。我们有时候也写作 $G^r$ 来表示 $r$ 是有根树 $G$ 的根。同时,对于一棵无根树,我们用 $G^r$ 来表示一棵有根树,这棵有根树是选择了它的一个节点 r 作为其根。我们用 $G^r_v$ 来表示有根树 $G^r$ 的一棵子树,这棵子树的节点均为 $v$ 的后代,它的根是 $v$ 。
当有一个同构关系在两棵有根树 $G^r$ 和 $H^s$ 之间,并且将 $r$ 映射到 $s$ 时,我们称是这两棵树是同构的。同样的,当有一棵 $G^r$ 的有根子树 $J^r$ 与 $H^s$ 同构时,我们写作 $H^s\subseteq_RG^r$。(注意到子树 $J^r$ 必须与 $G^r$ 有相同的根)
我们定义一个图 $G$ 中节点 $v$ 的开社区(open neighborhood)为 $N(v)={u:uv∈E}$,定义闭社区(closed neighborhood) 为 $N[v]=N(v)∪ \lbrace {v} \rbrace$。我们使用 $d_G(v)$来表示节点 $v$ 在图 $G$ 中的度(或者 $d(v)$ 当图 $G$ 指明的情况下)。
一个 $O(k^{1.5}n)$ 的算法
在这一节我们描述了一个 $O(k^{1.5}n)$ 算法,使之为在章节4和5中所改进的算法作基础。它建立在 Chung 的算法基础,与之拥有相同的渐进时间复杂度,但是它相比于 Chung 的算法更加简单,因为 $G$ 树只被遍历了一次(Chung 的算法遍历了两次)。我们简短地描述一下算法的完备性。我们注意到在第4和5节的改进也同样可以运用至 Chung 的原始算法。简单起见,我们描述一个算法来讨论这个问题,它也能很简单地扩展被用于搜索问题。
我们设 $G=(V,E)$ 和 $H=(V_H,E_H)$ 是输入的树(不失一般性,$|V_H|>1$)。选择 $G$ 的一个节点 $r$ 作为其根。我们希望知道对于每一个 $v∈V$ 和 $u∈V_H$ 是否有 $H^u \subseteq_RG^r_v$ 。为了计算这个的效率,我们也需要知道对于每个 $u$ 的邻居 $w$ 是否有 $H^w_u\subseteq_RG^r_v$(注意到 $H^w_u$ 是图 $H^u$ 删去 $H^u_w$ 得到的)。这个信息是重要的,因为 $H^u\subseteq_RG^r_v$ 当且仅当 $u$ 的每一个儿子 $u’$ 都有 $v$ 的唯一的儿子 $v’$ 使得 ${H^u_{u '} \subseteq_RG^r_{v '} }$ 。更加广泛地说,我们得到如下引理:
引理2.1:对于每一个 $G^r$ 中的节点 $v$ ,每一个 $H$ 中的节点 $u$ 和一个 $w∈N[u]$ 的节点 $a$,如果对 $H^w_u$ 中每一个 $u$ 的孩子 $u’$ 都有在 $v$ 唯一的孩子 $v’$,即 $H^u_{u’} \subseteq_RG^r_{v’}$ ,那么我们有 $H^u_{u’} \subseteq _RG^r_v$。
我们将这个信息存进集合 $S(v,u)$ 中,定义如下:对任意 $v \in V$ 和 $u \in V_H$ 有:$$ S(v,u)=\lbrace w \in N[u]:H^w_u \subseteq_RG^r_v \rbrace$$
我们看图2作为这个定义的例子。注意到(1) $u \in S(v,u)$ 当且仅当 $H^u=H^u_u \subseteq_RG^r_v$,(2) $u \in S(v,u) $ 意味着 $S(v,u)=N[u]$,(3)$d(v)<d(u)-1$ 意味着 $S(v,u)=\phi$。
这个算法计算了所有的 $u$ 和 $v$ 的 $S(v,u)$ 。我们将展示如何通过从根到叶地遍历 $G^r$ 中的所有节点 $v$ 并计算所有的 $u \in V_H$ $S(v,u)$ ,以此归纳计算 $S(v,u)$ (这个算法也在第三章使用伪代码进行了描述)。这个归纳法的基础是当 $v$ 是 $G^r$ 的叶子节点。 然后 $S(v,u)$ 就可以以下述方法计算所有的 $u$ :如果 $u$ 是 $H$ 的叶子,那么 $S(v,u)$ 就是由一个 $H$ 中只有单邻居的节点 $u$ 所组成的了。否则,如果 $u$ 是一个内部顶点, $S(v,u)$ 为空。
叶子节点:没有子节点的节点
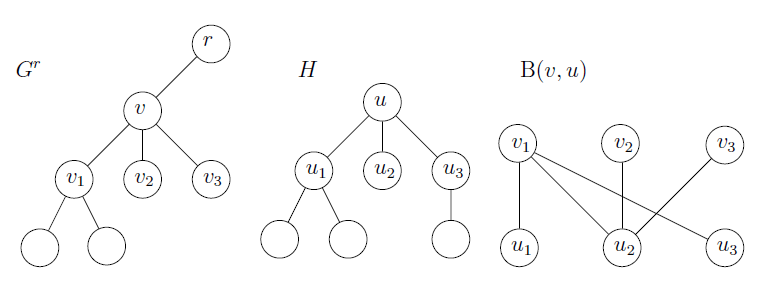
对于归纳步骤,考虑一个内部点 $v$(根据(3)我们可以假设 $d(v) \geq d(u)-1$)。我们首先需要计算对于所有的 $u \in V_H$ 所有 $v$ 的儿子 $v’$ 的$S(v’,u)$。然后,为了判断是否对于 $w \in N[u]$ 有 $w \in S(v,u)$,我们构造一个二部图 $B_w(v,u)$,它由两部分构成:$X^{v,u}_w$ 和 $Y^{v,u}$,其中 $X^{v,u}_w$ 是 $H^w_u$ 中节点 $u$ 的孩子集合,$Y^{v,u}是 $v$ 的孩子集合$,${u’v’}$ 是图 $B_w(v,u)$的一条边当且仅当 $H^u_{u’} \subseteq_RG^r_{v’}$(也即是说当且仅当 $u \in S(v’,u’)$)。根据引理2.1,$w$ 在 $S(v,u)$ 中当且仅当 $B_w(v,u)$ 有一个大小为 $|{X^{v,u}_w}|$ 的匹配。因此,为了计算 $S(v,u)$ 我们需要在 $d(u)+1$ 的二部图中找到最大的匹配。不过,所有的这些图都彼此相似:每一个图 $B_w(v,u)(w \not= u)$ 都是通过从图 $B_u(v,u)$ 中删去节点 $w$ 来得到。在第3节(推论3.2)中我们将证明只在图 $B_u(v,u)$ 中寻找最大匹配是足够的,然后我们可以有效地计算出所有满足 $w\not=u$ 在 $B_w(v,u)$ 中最大匹配的大小。在接下来的部分,我们将使用 $B(v,u)$ 而非 $B_u(v,u)$。看图2来找寻一个关于 $S(v,u)$ 和 $B(v,u)$ 关系的例子。
子树同构算法将在图3以伪代码形式进行展示。
定理2.2:子树同构算法以 $O(k^{1.5}n)$ 的时间复杂度和 $O(kn)$ 的空间复杂度解决子树同构问题
证明:算法的正确性来源于引理2.1。让我们考虑下空间复杂度。设 $V=\lbrace x_1,\dots,x_n \rbrace$, $V_H=\lbrace y_1,\dots,y_n\rbrace$。由于每一个集合 $S(v,u)$ 都是 $N[u]$ 的子集,我们可以使用一个大小为 $|{N[u]}|$ 二元向量 $A(v,u)$ 来维护 $S(v,u)$。同时,我们也可以维护一个 $k\times k$ 的矩阵 $I$,其中 $I(u,w)$ 是在向量 $A(v,u)$ $w \in N[u]$ 的索引号。换言之,$w \in S(v,u)$ 当且仅当比特编号 $I(u,w)$ 在 $A(v,u)$ 中是一个集合。因此空间复杂度是 $O(k^2+\sum^k_{j=1}{d(y_i)n})=O(kn)$ 并且每一次对 $S(v,u)$ 的访问花费的是常数时间。

- 选择 $G$ 一个节点 $r$ 作为 $G$ 的根节点
- 对于所有的 $u \in H$ 和 $v \in G$ 将 $S(v,u)$ 设为 $\phi$
- 对于 $G^r$ 中所有的叶子 $v$ 执行:
- 对于 $H$ 所有的叶子 $u$ 将 $N(u)$ 添加进 $S(v,u)$
- 对处于后序遍历的 $G^r$ 所有的内部节点 $v$ 执行:
- 设 $v_1,\dots,v_t$ 为 $v$ 的孩子
- 对于 $H$ 所有度不超过 $t+1$ 的节点 $u=u_0$执行:
- 设 $u_1,\dots,u_s$ 为 $u$ 的邻居
- 构造二部图 $B(v,u)=(X,Y,E_{vu})$,其中 $X=\lbrace u_1,\dots,u_s\rbrace$,$Y=\lbrace v_1,\dots,v_t\rbrace$,$E_{vu}=\lbrace u_iv_j:u\in S(v_j,u_i)\rbrace$ 使用如下表示:$X_0=X$ $X_i=X-\lbrace u_i \rbrace$
- 对于所有的 $0 \leq i \leq s$ 计算大小 $m_i$,找到 $X_i$ 和 $Y$ 之间的最大匹配。
- 将 $\lbrace u_i:m_i=|{X_i}|,0 \leq i \leq s\rbrace$ 添加进 $S(v,u)$
- 如果 $u \in S(v,u)$ 那么答案是是,停止。
- 循环结束标识对应第7行
- 循环结束标识对应第5行
- 答案是否
至于算法的空间复杂度,关键在于第10步。它计算了一些图中的最大匹配的规模。因为这些图都是高度相关的,我们能够在第3节中得到:计算它们的最大匹配的大小可以在计算单个最大匹配的同一时间内完成。因此,我们使用推论3.2执行算法的第10步,因此其时间复杂度的主要部分是第10步确定图 $B(x_i,y_i)$ 对于所有的 $i$,$j$的讨论。使用 Hopcroft 和 Karp 的算法找出一个 $B(x_i,y_i)$ 的最大匹配花费的时间是 $O(d(y_i)^{1.5}d(x_i))$(或者 Dinic 的等效算法)因此花费在处理节点 $x_i$ 上的时间最多是 $O(\sum^k_{j=1}{d(y_j)^{1.5}d(x_i)}=O((2k)^{1.5}d(x_i))$。因此,总时间复杂度为 $O(k^{1.5}n)$
我们注意到上述算法可以被用于解决子树同胚问题而不需要改变渐进的复杂度。对算法的相同修改应用在后面的章节。
在拓扑学中,同胚(homeomorphism、topological isomorphism、bi continuous function)是两个拓扑空间之间的双连续函数。同胚是拓扑空间范畴中的同构;也就是说,它们是保持给定空间的所有拓扑性质的映射。如果两个空间之间存在同胚,那么这两个空间就称为同胚的,从拓扑学的观点来看,两个空间是相同的。
两个拓扑空间 $\lbrace X,T_X \rbrace$ 和$\lbrace Y,T_Y \rbrace$之间的函数 $f:x \to y$ 称为同胚,如果它具有下列性质:
$f$ 是双射(单射和满射);
$f$ 是连续的;
反函数 $f^{-1}$ 也是连续的( $f$ 是开映射)。
满足以上三个性质的函数有时称为双连续。自同胚就是从一个拓扑空间到它本身的同胚。同胚形成了所有拓扑空间的类上的等价关系。所得到的等价类称为同胚类。
——引自维基百科
匹配
在这一节,我们给出了几个关于匹配的引理,这些引理对于得到更有效的子树同构问题是必须要的。对于接下来的引理,我们设 $B=(X,Y,E)$ 是一个二部图,其中 $X=\lbrace x_1,\dots,x_s\rbrace$,$Y=\lbrace y_1,\dots,y_t\rbrace$ 并且 $s \leq t+1$。对于 $1 \leq i \leq s$,用 $X_0=X$ 和 $X_i=X-\lbrace x_i \rbrace$ 进行表示。对于 $0 \leq i \leq s$,令 $m_i$ 表示在 $X_i$ 和 $Y$ 之间最大的匹配。显然对于任意的 $i \geq 1$,有 $m_i=m_0$ 或是 $m_i=m_0-1$。
一个匹配中重要的概念就是临界点。对于图 $G$ 中的一个节点 $x$,当在 $G-x$ 的最大匹配严格小于在 $G$ 中的最大匹配时,我们说 x 是临界的(也即是说 $x_i$ 是临界的当且仅当 $m_i=m_0-1$)。设 $M$ 是 $B$ 的最大匹配。我们定义一个有向图 $B_M$,使 $B_M=(X\cup Y,E_M)$ ,其中有$$E_M=\lbrace (x,y):xy \in E-M,x \in X,y \in Y\rbrace \cup \lbrace (y,x):xy \in M,x \in X, y\in Y \rbrace$$
我们用 $X_M$ 表示所有 $X$ 中的不与 $M$ 匹配的节点。
引理3.1:对于 $B$ 中每一个最大匹配 $M$,和任意 $x_i \in X$,$x_i$ 临界(即是 m_i=m_0-1)当且仅当 $x_i$ 在 $M$ 中匹配并且在 $B_M$ 不存在一条路径能够从 $X_M$ 到 $x_i$。
证明:(充分性)我们用反证法进行证明。如果 $x_i$ 在 $M$ 中不匹配,那么 $M$ 就是在 $X_i$ 和 $Y$ 之间,因此有 $m_i=m_0$,矛盾($m_i=m_0-1$)。当然,如果 $B_M$ 有一条从 $X_M$ 到 $x_i$ 的路径 $P$,那么 $M\Delta P(=M \cup P-M\cap P)$ 就是一个 $x_i$ 不匹配的最大匹配,我们再一次得到了 $m_i=m_0$ 的矛盾。
(相反地),从矛盾开始假设,设 $m_i=m_0$。设 $y$ 是在 $M$ 中匹配 $X-i$ 的节点。又 $|{M-\lbrace x_iy \rbrace}|=m_0-1 < m_i$,$M-\lbrace x_iy \rbrace$ 不是一个在 $X_i$ 和 $Y$ 之间的最大匹配,并且在 Berge 的理论中,存在一条增广路径 $P$ 到达 $X_M$ 中的一个节点 $x_j$,另一个节点是 $y$ (因为如果另一个是 $Y$ 中节点且在 $M$ 中不匹配的话,$P$ 就是 $M$ 的一条增广路径)。但是这意味着一条在有向图 $B_M$ 中的从 $x_j$ 到 $x_i$ 的路径,矛盾。
增广路径:若P是图G中一条连通两个未匹配顶点的路径,并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广路径。
推论3.2:给定一个 $B$ 的最大匹配 $M$,我们可以在 $O(st)$ 的时间内计算出 $m_i$ 的值,其中 $0 \leq i \leq s$。
证明:构造图 $B_M$ 并且找到所有从 $X_M$ 可达到的节点,这可以在 $O(st)$ 的时间内使用深度优先搜索完成。然后应用引理3.1。对于任意一个 $x_i$,如果 $x_i$ 在 $M$ 中匹配且不可从 $X_M$ 到达,我们设 $m_i=|M|-1$,否则 $m_i=|M|$。
深度优先搜索算法(英语:Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点 $v$ 的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
引理3.3:在 $B$ 中找到一个最大匹配的问题可以被缩减到 $O(st)$ 的时间变成找到 $B$ 的一个子图的最大匹配,其中该子图拥有最多 $s^2$ 条边和节点,节点的最大度为 $s$。
证明:设 $X’$ 是所有的 $X$ 中度小于 $s$ 的节点集合。设 $B’$ 是由 $X’$ 及其邻居从 $B$ 中导出的子图。构建 $X’$ 和 $B’$ 花费 $O(|X|+|Y|+|E|)=O(st)$ 的时间。我们说给定 $B’$ 的最大匹配 $M’$,我们可以构建一个 $B$ 的最大匹配 $M$:首先将 $M’$ 中的所有边添加至 $M$。对于 $X-X’$ 中的每一个节点,找到 $Y$ 中的一个不匹配的邻居 $y$ 然后将 $xy$ 添加到 $M$(这样一个节点 $y$ 一定存在,因为这样的 $x$ 拥有至少 $s$ 个邻居并且至多 $s-1$ 个邻居是匹配的)。找到 $x$ 的一个不匹配邻居花费 $O(s)$ 的时间,因此构建 $M$ 花费 $O(s^2)$ 的时间。
一个 $O(\frac{k^{1.5}}{\log k}n)$ 的算法
我们现在来对章节2中的算法进行 $\log k$ 因子的改进。我们使用之前的算法,但是如果我们通过利用二部图的团划分思想及其在最大匹配中的应用,将会在解决最大匹配问题时更加高效。Feder 和 Motwani 的算法最初是针对具有相同大小部分的二部图提出的,可以推广到一般的二部图。这使得我们可以给出时间复杂度为 $O((k^{1.5}/\log k)n)$ 的子树同构算法。我们不去描述对 Feder 和 Motwani 算法的修改,我们这里给出一个更简单的方法来得到一个 $O((k^{1.5}/\log k)n)$ 时间的子树同构算法。相比之下,[16](参考文献,这里不列出)利用了图的稠密性,而我们利用子树同构算法中必须解决的匹配问题的特殊结构,实现了时间复杂度的降低。
修改后的算法,叫做改良子树同构(Improved-Subtree-Isomorphism),和子树同构算法一样,但不同在于我们在处理第10步时采用了不同的方法。设 $v$ 是 $G^r$ 中的一些节点,它们的孩子是 $v_1,\dots,v_t$,设 $u$ 是 $H$ 中的一个节点,它的孩子是 $u_1,\dots,u_s$。我们现在考虑找到一个 $B=B(v,u)$ 中的最大匹配。回忆起来 $B=(X,Y,E)$ 其中 $X=\lbrace u_1,\dots,u_s\rbrace$, $Y=\lbrace v_1,\dots,v_t\rbrace$。我们假设 $s\leq t+1$ (否则 $S(v,u)=\phi$)
我们首先应用引理3.3来构建一个 $B$ 的子图 $B’=(X’,Y’,E’)$,令其最大度为 $s$。然后,像在[16]中那样,我们将 $B’$ 的边划分到二部图 $C_1,\dots,C_p$ 中。我们按以下方法进行划分:首先,我们以字典序对 $X’$ 中的节点进行排序,其中节点 $u$ 的键值为 $N[u]$ 。然后,我们将 $X’$ 分成相同的键 $X^1,\dots,X^p$,(也即是说,所有的 $X^i$ 中的节点都在 $Y’$ 中由相同的邻居)。现在,对于所有的 $1\leq i\leq p$,我们设 $C_i$ 是去掉了 $X^i$ 节点的子图,并且它所有的邻居都在 $Y’$ 中。我们现在按照[16]中的方法构建一个网络 $B^\ast$,它的节点为 $V^\ast =X’\cup Y’ \cup \lbrace c_1,\dots,c_p,a,b\rbrace$。边为 $E^\ast =E_1\cup E_2$,其中有:
$$E_1=\lbrace au_i:u_i\in X’\rbrace \cup \lbrace v_ib:v_i \in Y’ \rbrace $$
$$E_2=\lbrace u_ic_j:j \leq p,u_i \in C_j\rbrace \cup \lbrace c_jv_i:j \leq p,v_i \in C_j \rbrace$$
所有的边的都有1的容量。源是$a$,汇聚到$b$。我们使用 Dinic 的算法在 $B^\ast$ 中找到一个最大流(积分),然后以此构建 $B’$ 中的最大匹配。(因为所有边的容量都是1,可以可以将流$f$分解为从$a$到$b$的边不相交路径,其中每条路径上的流为1。因为每一条路径都符合 $[a,u_i,c_k,v_j,b]$的格式,我们可以通过提出一条边 $u_iv_j$ 来对应那条路并定义 $B’$ 中的一个匹配。这种匹配的极大性来自于流的极大性。)
我们现在分析上述算法的时间复杂度。我们用 $D(u)$ 来表示在森林 $H^u_{u_1},\dots,H^u_{u_s}$ 中不同的树。
引理4.1:改良子树同构算法在 $B(v,u)$ 中找到一个最大匹配的时间在 $O(st+ts^{0.5}D(u))$ 以内。
证明:注意到如果对于某些 $i,j$,有根树$H^u_{u_i}$ 和 $H^u_{u_j}$ 是同构的,那么在 $B=B(v,u)$ 中节点 $u_i,u_j$ 完全拥有相同的邻居,并且在 $B’$ 中亦是如此(假设 $u_i$ 和 $u_j$ 在 $B’$ 中未被删去)。因此有 $p\leq D(u)$。
构造 $B,B’,B^\ast$ 的时间是 $O(st)$(我们使用基数排序对 $X’$ 节点进行排序)。我们现在限定了在 $B^\ast$ 中找到最大流的时间:$E_1$ 的大小为 $|{X’}|+|{Y’}|$,其中$|{X’}|\leq s$,$|{Y’}|\leq sp$ (因为每一个 $Y’$ 中节点拥有至少一条来自 $c_j$ 的边,不超过 $s$ 条边从每个顶点 $c_j$ 到$Y’$ 中的顶点)。$E_2$ 的大小至少是 $2sp$,因为 $E_2$ 中某顶点$c_j$上的入射边数最多为$|{X’}|+d_{B’}(u_i)\leq 2s$,其中 $u_i \in C_j$。因此,$B^\ast$ 中的边数为$O(sp)$。在$B^\ast$中的顶点数至多为$s+t+p+2=O(t)$,因为 $s\leq t+1$。现在,Dinic 的算法表现出$O(\sqrt{|{V^\ast}|})$ 的阶数,每一阶花费 $O(|{E^\ast}|)$ 的时间。因此,总时间复杂度为 $O(t^{0.5}sp)=O(ts^{0.5}p)=o(ts^{0.5}D(u))$
我们再次用 $V$ 表示 $\lbrace x_1,\dots,x_n\rbrace$,$V_H$ 表示 $\lbrace y_1,\dots,y_k\rbrace$。通过引理4.1,改良子树同构算法的时间复杂度为:
$$O(\displaystyle \sum^n_{i=1}{\displaystyle \sum^k_{j=1}{d(y_j)d(x_i)+d(x_i)d(y_j)^{0.5}D(y_j)}})=O(kn+n\displaystyle \sum^k_{j=1}{d(y_j)^{0.5}D(y_j)})$$
我们将限制求和 $\sum^k_{j=1}{d(y_j)^{0.5}D(y_j)}$ 到 $O(k^{1.5}/\log k)$。
我们首先需要一个简单的组合引理。令 $g(n)$ 表示 $n$ 个节点的不相同(也即是不同构)有根树的数量。我们可以使用以下结果:
引理4.2:$g(n)=2^{\Theta (n)}$
设 $f(n)$ 表示最大的 $n$ 节点森林中的不同构有根树的数量。
引理4.3:$f(n)=\Theta (n/\log n)$
证明:为了展示下限,我们使用结论:对于足够大的 $n$ ,有$g(n) \geq 2^n$。 因此,不同的$l=\lfloor \log \frac{n}{\log n}\rfloor$节点有根树的数量$g(l)\geq 2^{\log \frac{n}{\log n}-1}=\frac{n}{2\log n}$。因此我们可以通过提出 $\lfloor \frac{n}{2\log n} \rfloor$ 个不同的拥有 $l$ 个节点的树俩构建森林,森林的总节点数是 $\lfloor \frac{n}{2\log n} \rfloor<n$。因此 $f(n)=\Omega (\frac{n}{\log n})$。我们现在来讨论上限。
如果我们有一个有根树的森林,并且用 $r_i$ 来表示森林中拥有 $i$ 个节点的树的数量,那么不同的树的数量最多为 $\sum^n_{i=1}min(r_i,g(i))$。因此有:
$$f(n)\leq max\lbrace \displaystyle \sum^n_{i=1}{min(r_i,g(i)):r_1,\dots,r_n \in \mathbb{N},\displaystyle \sum^n_{i=1}{ir_i \leq n}} \rbrace$$
根据引理4.2,有:
$$f(n)\leq max\lbrace \displaystyle\sum^n_{i=1}{min(r_i,c^i):r_1,\dots,r_n\in \mathbb{N},\displaystyle\sum^n_{i=1}{ir_i}\leq n} \rbrace$$
对于一些整数常量 $c$。我们设 $x$ 是最小的整数,使得 $\sum^x_{i=1}{ic^i}\geq n$。设 $r_1,\dots,r_n$ 为在 $\sum^n_{1}{ir_i}\leq n$ 约束下使得 $\sum^n_{i=1}{min(r_i,c^i)}$ 最大化的一组值。我们可以假设 $r_i\leq c^i$ 对于所有 $i$ 成立,因为如果对于某些 $j$ 有 $r_j > c^j$ 的话,我们可以设 $r_j=c^j$,然后 $\sum^n_{i=1}{min(r_i,c^i)}$ 的值并未改变。现在,考虑对于某些 $j>x$ 的情况 $r_j>0$。这表明存在一个 $k\leq x$ 使得 $r_k<c^k$(否则 $\sum^n_{i=1}{ir_i}\geq \sum^x_{i=1}{ir_i+jr_j}=\sum^x_{i=1}{ic^i+jr_j}>n$,矛盾)。如果我们将 $r_j$ 减一,$r_k$ 加一,$\sum^n_{i=1}{min(r_i,c^i)}$ 的值并未改变,而且限制条件 $\sum^n_{i=1}{ir_i}\leq n$ 仍然满足(因为$k<j$)。我们可以重复这个过程直到 $r_j=0$ 对于所有的 $j>x$ 都成立,因此有:
$$f(n)\leq\displaystyle\sum^n_{i=1}{min(r_i,c^i)}\leq\displaystyle\sum^x_{i=1}{c^i}=O(c^x)$$
这个引理根据以下结论得到:$x=\log_cn-\log_c\log_cn+O(1)$。
我们现在继续分析改良子树同构算法。设 $\epsilon$ 是一个常数,且 $0<\epsilon<\frac{1}{3}$。如果一个节点的度至少有 $2k^{1-\epsilon}$ 则我们称 $H$ 的一个节点是重的,否则称之为轻的。显然,重节点至多有 $k^\epsilon$ 个。如果 $u$ 是一个重节点并且 $v$ 是其一个邻居,这样的 $H^u_v$ 不包含重节点,那么我们称每一个在 $H^u_v$ 中的节点叫 $u$ 私有节点(private vertex)。我们用 $l_j$ 来表示重节点 $y_j$ 的私有节点数。
引理4.4:对每一个重节点 $y_j$,都有 $d(y_j)\leq k^\epsilon+l_j$ 和 $D(y_j)\leq k^\epsilon+f(l_j)$
证明:设 $u_1,\dots,u_p$ 为 $y_j$ 的邻居中的私有节点,设 $v_1,\dots,v_q$ 是 $y_j$ 剩下的节点。显然,$p$ 是 $y_j$ 的私有节点数 $l_j$ 的上界。此外,对于每一个节点 $v_i$ 我们可以选择一个 $H^{y_j}_{v_i}$ 中的重节点 $w_i$。因为我们选择的节点不同,我们可以得到 $q$ 是小于重节点数的。因此有 $D(y_j)\leq q+f(l_j)\leq k^\epsilon+f(l_j)$。
引理4.5:我们把 $\sum^k_{j=1}{d(y_j)^{0.5}D(y_j)}$ 分成两个和。将 $H$ 的轻节点相加我们得到:
$$\displaystyle\sum_{j:y_j\,is\,light}{d(y_j)^{0.5}D(y_j)}\leq \displaystyle\sum_{y_j\,is\,light}{d(y_j)^{1.5}}\leq (2k^{1-\epsilon})^{0.5}\displaystyle\sum_{j:y_j\,is\,light}{d(y_j)}$$
$$\leq (2k^{1-\epsilon})^{0.5}2k=2^{1.5}k^{1.5-\epsilon/2}$$
最后一个不等式从 $\sum^k_{j=1}{d(y_j)}=2k-2$ 得到。
求和所有的重节点,应用引理4.4我们得到:
$$\displaystyle\sum_{j:y_j\,is\,heavy}{d(y_j)^{0.5}D(y_j)}\leq \displaystyle\sum_{j:y_j\,is\,heavy}{(k^{\epsilon/2}+l^{0.5}_j)(k^\epsilon+f(l_j))}$$
因为 $f(l_j)\leq l_j\leq k$,并且重节点数至多为 $k^\epsilon$,我们有:
$$\leq \displaystyle\sum_{j:y_j\,is\,heavy}{(k^{3\epsilon/2}+k^{0.5+\epsilon}+k^{1+\epsilon/2}+l^{0.5}_jf(l_j))}$$
$$3k^{1+3\epsilon/2}+\displaystyle\sum_{j:y_j\,is\,heavy}{l_j^{0.5}f(l_j)}$$
又根据引理4.3,有结论 $\sum_{j:y_j\,is\,heavy}{l_j}\leq k$(因为每一个节点都最多只可能是1个重节点的私有节点),并且函数 $h(x)=x^{1.5}/\log x$ 是凸函数,我们有:
$$\leq 3k^{1+3\epsilon/2}+\displaystyle\sum_{j:y_j\,is\,heavy}{c\frac{l_j^{1.5}}{\log l_j}}\leq 3k^{1+3\epsilon/2}+c\frac{k^{1.5}}{\log k}$$
我们因此证明了一下定理:
定理4.6:改良子树同构算法在 $O((k^{1.5}/\log k)n)$ 时间内解决子树同构问题。
一个 $O(k^{1.376}n)$ 的算法
在本节中,我们给出了一种求解子树同构决策问题的随机算法。该算法在渐近性方面比上一节的确定性算法更有效。
相同的,这个随机化子树同构(Randomized-Subtree-Isomorphism)基于子树同构算法,但是在最大匹配问题的解决上有所不同。考虑 $G^r$ 中的一些节点 $v$,它们的孩子是 $v_1,\dots,v_t$,并且 $H$ 中一些节点 $u$ 的邻居是 $u_1,\dots,u_s$。我们使用 Cheriyan 的算法来找到 $B(v,u)$ 最大的匹配然后找到所有的 $B(v,u)$ 中的关键节点(Critical vertices)。
Cheriyan 的寻找关键节点算法如下:给定一个输入图 $G=(V,E)$,其中 $V=\lbrace 1,2,\dots,n\rbrace$,选择一个大的素数 $q$ 并构建一个 $n\times n$ 矩阵 $C$,构建方法如下:对于每一条 $E$ 中的边 $ij$,一致地从 $\lbrace1,2,\dots,q-1 \rbrace$ 选择一个随机数 $w_{ij}$ 。设 $c_{ij}=w_{ij},c_{ji}=-w_{ij}$。将 $C$ 中所有的其他元素设置为0。最后,求出 $C$ 的零空间在 $Z$ 上的基底$a_1,\dots,a_r$。接下来,高概率会有:对所有 $i\in V$,$G$ 中最大匹配的大小与 $(n-r)/2$ 相同,节点 $i$ 是关键的当且仅当所有的第 $i$ 个节点的基 $a_1,\dots,a_r$ 为0。
又因为图 $B(v,u)$ 是一个二部图,当应用 Cheriyan 的算法于 $B(v,u)$ 时,矩阵 $C$ 符合以下形式:
$$
C=
\begin{bmatrix}
0 & {C’} \\
{C’’} & 0 \\
\end{bmatrix}
$$
在这里,$C’$ 是一个 $t\times s$ 块,$C’’$ 是一个 $s\times t$块。因此,我们可以通过求 $C’$ 和 $C’’$ 的零空间的基来求出 $C$ 的零空间的基。这可以在 $O(s^{\omega-1}t)$ 时间内完成,其中 $\omega$ 表示矩阵乘法的指数。因此,随机化的子树同构算法运行时间是 $O(\sum^n_{i=1}{\sum^k_{j=1}{d(y_j)^{\omega -1}d(x_i)}})=O(k^{\omega -1}n)$
定理5.1:随机化子树同构算法预计在 $O(k^{\omega -1}n)$ 时间内求解决策问题。
又 $\omega <2.376$,我们有
推论5.2:随机化子树同构算法在 $O(k^{1.376}n)$ 期望时间内求解决策问题
感谢
我们作者感谢匿名审稿人对手稿的仔细阅读和许多有益的评论。
笔者感谢有道翻译提供的支持。(笑)
参考文献
(仅列出提到的那几个人的)
- M. J. Chung. $O(n^{2.5})$ time algorithms for the subgraph homeomorphism problem on trees. J. of Algorithms, 8:106-112, 1987.
- T. Feder and R. Motwani. Clique partitions, graph compression and speeding-up algorithms. In Proc. 23rd Symposium on the Theory of Computing (STOC 91), pages 123-133. ACM press, 1991.
- J. E. Hopcroft and R. M. Karp. A $n^{5/2}$ algorithm for maximum matching in bipartite graphs. SIAM J. Computing, 2:225-231, 1973.
- J. E. Hopcroft and R. E. Tarjan. Isomorphism of planar graphs. In Raymond E. Miller and James W. Thatcher, editors, Complexity of Computer Computations, pages 131-152. Plenum Press, 1972.
- J. Cheriyan. Randomized $\tilde{O}(M(|V|))$ algorithms for problems in matching theory. SIAM J. Computing, 26:1635-1655, 1997.
太多了,略,共计42篇参考文献。
